평균과 분산 Review
이전 포스팅에서 평균과 분산에 대해서 학습했기에 해당 식만 상기시켜 보자.


Geometric distribution
이 분포에서는 확률변수를 다르게 정의한다. K라는 확률변수는 어떠한 사건을 첫 번째로 성공할때까지의 순서로 정의된다.
예를 들어 주사위를 던진다고 할 때, 처음으로 6이라는 숫자가 나올 경우를 생각해보면, 확률변수와 확률은 다음과 같이 정의된다.
즉 다음과 같이 정의된다. 첫번째 사건이 반드시 일어나야 하므로 k는 1부터 시작한다.

(a) 사건의 횟수를 무한으로 발생시킨다면?

(b) 만약 P=1/3이라면, 적어도 3번은 시행해봐야 한다.
(c) 평균을 구해보자.

k는 상수이므로,

식을 미분을 해보자.

결국 결론은 다음과 같다.

(d) 분산

(c)에서 미분 한 식을 한번 더 미분한다.

양 변에 p(1−p)를 곱한다.
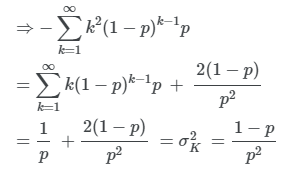
평균과 분산의 수학적인 의미?
그렇다면 우리가 여태 학습한 평균과 분산은 수학적인 의미에서 어떤의미를 갖는지 알아보자.
Facebook의 얼굴 인식 태그 기능을 구현하고자 한다. 그렇다면 수많은 사진들 중에서 얼굴이라고 판단되는 부분을 Detection해야한다. 그렇다면, 판단은 어떻게하고 어떤 기준으로 해야할까?
우리는 그에 대한 선택의 근거가 존재해야한다. 그 근거는 무엇일까?
공학도로써 판단의 기준은 함수나 숫자가 되어야 한다.
표준적인 참값인 Ground Truth(GT)가 있고 사진의 predict value가 있다고 해보자. 그럼 그에 대한 에러는

로 나타낼 수 있다. 여기서 제곱이 들어간 이유는 GT가 특정 값이 아니라 벡터일 수 있기 때문이다.
즉, 판단과 선택의 기준은 수치 모델에 해당해야한다.
위의 Error 모델을 활용하여 예를 들어 생각해보자. 다음과 같은 함수에서 minimum을 갖는 x 값은 무엇일까?

이 정도는 뭐.. 쉽게 생각 할 수 있다. x=a_1에서 minimum 값을 가진다. 그렇다면 다음 함수는?

잠깐 멈칫하고 생각을 해보면, (a1 +a2)/2에서 min값을 가지는 것을 알 수 있다. 그 다음으로,

뭔가 슬슬 감이 온다. 잘 모르겠다면, 글의 흐름상 (a1 +a2 +a3)/3이 될 것 같지 않은가?
그렇다면 a의 갯수가 n개 일 때를 생각해보자.

를 hat{x}이라고 한다면,

위의 사건이 discrete한 확률변수라고 했을 때, f(x)의 각 항에 확률 값을 곱할 수 있다. 놀랍게도, Error 모델이 최솟값을 가지게 하는 x값은 평균이 되고, 평균을 함수에 대입했을 때 나오는 값은 분산이 된다.

자 여기서 분산이라함은 data가 얼마나 퍼져있느냐를 나타내는 것이다. 그렇다면, 분산이 가지는 의미를 다시 한 번 되새겨볼 수 있다.
Median (data들의 중간값)
평균과 중간값의 의미를 구분할 필요가 있다. 만약 1, 2, 4, 5 ,7이라는 숫자가 있다. 이 숫자들의 평균은 3.8이고 중간값은 4이다.
이번엔 g(x)라는 새로운 함수해서 알아보자.

이 함수의 중간값은 a1이 될 것이다.

이 함수의 중간값은 그래프를 그려보면 알 수 있는데,

a1과 a2 사이의 모든 값에 해당하는 값들이 중간값이 될 수 있다. 마찬가지로 ,


이런식으로 최소값을 가지는 지점은 그 함수의 중간위치인 것을 알 수 있다.
Conditional Mean
Event A라는 특정한 조건이 주어졌을 때의 RV X의 평균는 다음과 같이 나타낼 수 있다.

확률 자체가 조건부 확률로 바뀌게 된다.
for continuous case,

'Mathematics(수학) > Probability and Statistics (확률과통계)' 카테고리의 다른 글
| [확률과통계] 지수분포와 어랑분포 (0) | 2023.06.15 |
|---|---|
| [확률과통계] 여러가지 이산 확률 분포 (0) | 2023.06.15 |
| [확률과통계] 확률변수의 평균과 분산 (0) | 2023.06.15 |
| [확률과통계] 이산확률변수와 연속확률변수 (0) | 2023.06.15 |
| [확률과통계] 확률변수의 정의 (0) | 2023.06.15 |