이전 포스팅 복습
평균. 즉, Expectation은 E[X]으로 나타낼 수 있다.
평균의 본질적인 의미를 알아보기 위해 Error 모델을 정의 했었다.
real observation을 hat{x}라고 하고 우리가 예측한 prediction 값을 x 라고 한다면,
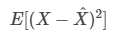
라고 정의했고, Error 모델을 촤소화 시키는 것이 평균이라고 했다. 그렇다면 mean(평균)이 갖는 의미를 확률적으로 나타내보자.
Cheryshev Inequality
쳬이셰프 부등식은 mean이 갖는 의미를 확률적으로 재해석하는 것이고, 식으로 나타내면.

확률 변수 X와 평균의 차이가 나는 기준을 a라고 했을 때, 그 차이가 a보다 클 확률을 나타낸것이다.
유도과정은 다음과 같다.

Special Distribution
Bernoulli Distribution
베르누이 분포에서 확률 변수는 binary(두 가지 outcome)으로 정의된다.
P(success) = p → 1
P(failure) = 1-p →
평균과 분산은 다음과 같이 정의된다.

Binomial Distrubution
이항 분포에서의 확률 변수는 다음과 같이 정의된다. 베르누이 분포를 가지는 Event를 총 n 번 시행하여, 그 중에서 원하는 결과를 얻은 횟수를 의미한다. 다음과 같은 식으로 정의할 수 있다.
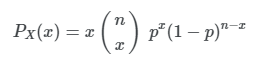
평균과 분산의 정의는 다음과 같다.
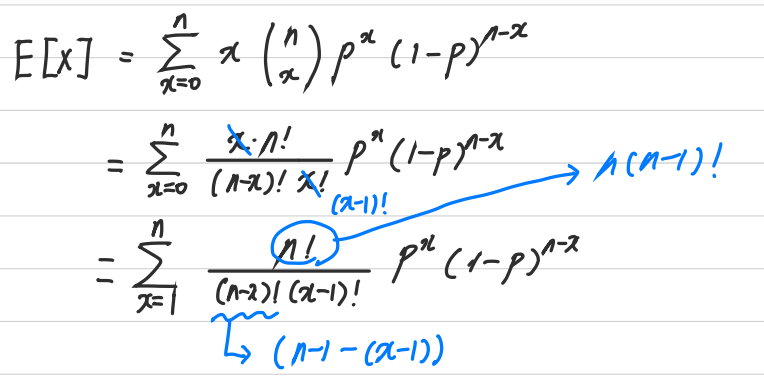


Geometric Distribution
기하 분포에서의 확률 분포는 어떠한 사건을 반복적으로 시행했을 때 첫번 째로 원하는 결과가 나올때까지의 횟수이다. 이전 포스팅에서 다뤘지만 기억해야할 특징이 하나가 있다.
주사위로 예를 들어 보자. 주사위를 던져서 본인은 6이라는 숫자가 나왔으면 한다. 던지다 보면 언젠가 나오겠지 하는 마음으로 계속 던졌는데 10번이 던져도 나오지 않았다. 당황하지 않고 5번 만 던져야지 했는데 또 나오지 않았다. 그렇다면 여기서 앞서 시행한 15번의 시행은 무시하는게 정신 건강에 좋을 것 같지 않나?
기하 분포에서는 무시해도 상관없다. 그 이유를 살펴보면 결국 CDF와 동일한 결과가 나온다.

'Mathematics(수학) > Probability and Statistics (확률과통계)' 카테고리의 다른 글
| [확률과통계] 드디어 나왔다. 가우시안 분포 (Gaussian Distribution) (0) | 2023.06.16 |
|---|---|
| [확률과통계] 지수분포와 어랑분포 (0) | 2023.06.15 |
| [확률과통계] 평균과 분산, 조건부확률 (0) | 2023.06.15 |
| [확률과통계] 확률변수의 평균과 분산 (0) | 2023.06.15 |
| [확률과통계] 이산확률변수와 연속확률변수 (0) | 2023.06.15 |